Games As Graphs I: Bridges of Shangri-La

Understanding Board Game Design via Graph Representations

This is a series on understanding various boardgames via graph representations, with this post focusing on the Bridges of Shangri-La by Leo Colovini¹.

¹ 

Image from BGG courtesy of @fungry

I’ve wanted to look at some games and write down mathematical descriptions for them. For me, this is a way to understand their design better, and also be a way to generate new ideas.

Since this is the first of several posts, I’ll describe some fundamentals of Graph Theory.

Graph Theory Primer

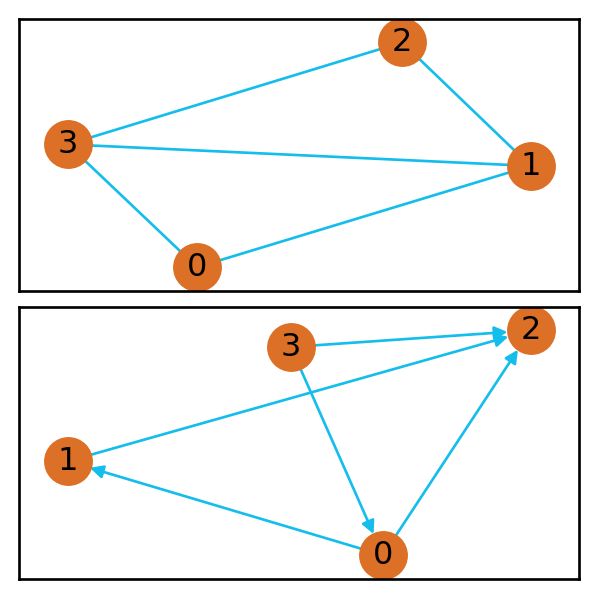
A graph \(G\) is a set of vertices \(V\) and a set of edges \(E \subset V \times V\). We can draw these graphs pretty easily Figure 1 .²³

² To differentiate the undirected and directed graph, we’d have to distinguish between ordered and unordered tuples, but I’m being intentionally not rigorous since the meaning is clear with pictures.

³ Note that a graph drawing is unique. We can move the edges and vertices around.

Figure 1: Graphs on 4 vertices

A graph where for all edges \((u, v) \in E, u \ne v\) is called a simple graph (edges with the same start and end points are called loops).

Graphs can come in an undirected or directed flavor. In a directed graphs, the edges have an orientation (Figure 1).

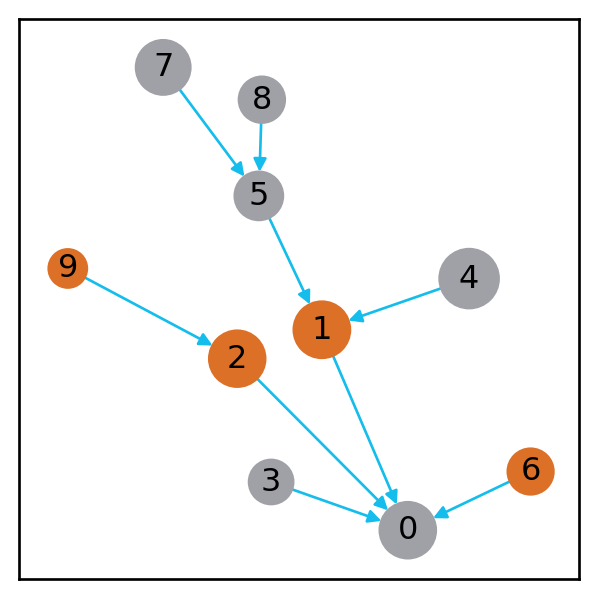
Edges and vertices may also have weights associated with them. These are typically used to assign costs. In general, different attributes can be assigned to an edge or vertex such as color (Figure 2).

Figure 2: A more complicated graph on 10 vertices. Vertices are scaled by their edge weight \(w\) and are colored one of two colors.

What does a graph represent? As much as limited by the imagination:

• The vertices \(V\) could represent locations, and edges \(E\) represent whether two locations are reachable from each other. This includes maps, road networks, but even things like chess positions for something like a Knight’s Tour.
• The vertices \(V\) are individuals, and the edges \(E\) represent contact. This could be used for something like a social network, but also disease modelling.
• For a directed graph \(G\) The vertices \(V\) are tasks, and the edges \(E\) represent which task has to be done before the next. This includes things like supply chain management.

After representing something as a graph, there are a variety of algorithms to deduce things about the graph. Some common problems include finding the shortest path, determining if there is a cycle, graph coloring, etc.

We won’t be needing these but may encounter these in future discussions.

Bridges of Shangri-La

Bridges of Shangri-La is a game by Leo Colovini for 3-4 players. It takes place on a map representing monasteries in Tibet.

Your goal is to have the most number of masters out on the board after all the bridges have collapsed. Each master is worth 1 point.

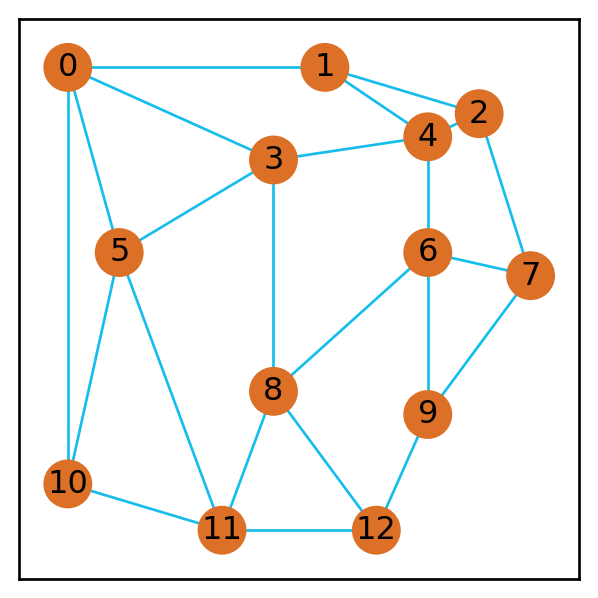
Before I give a rough summary of the rules, I’ll depict the board as a map for simplicity of discussion ⁴.

⁴ This is the 4P map. The top right corner is excluded for the 3P game.

Figure 3: Bridges of Shangri-La map as a graph.

Each vertex represents a village, and each edge represents a bridge. Each village also has 7 spots for the 7 different types of masters ⁵.

⁵ 

Example of placing masters

At the very beginning of the game, each player will place one of each type of master (in their player color) into villages of their choice. That will be 7 placements for each player. Each spot is exclusive.

On a players’ turn they have one of three actions:

1. Place a master: You can only do this in a village where you have a master of your color and if there is an unoccupied space.

2. Recruit students: You can place up to 2 students. You place a master tile on a master you already have, with the top tile called a student. Each master can only have one student.

3. The Journey of the Students: Choose two connected villages, and one of them being the one travelled from (“attacker”) and the other the (“defender”). The village that has the most tiles is considered stronger (with the village with the most masters and then “defender” breaking ties).

   • If the “attacker” is stronger, than all students in the “attacking” village move over to the “defender”, occupying their corresponding space (removing opponents tiles if they are occupied).
   • If the “defender” is stronger, than students only move over to empty spots, and otherwise get discarded.
   • Afterwards, the bridge between the two villages gets destroyed.

Once all bridges are destroyed the game ends, with the player with the most masters on the board winning.

Graph Representation

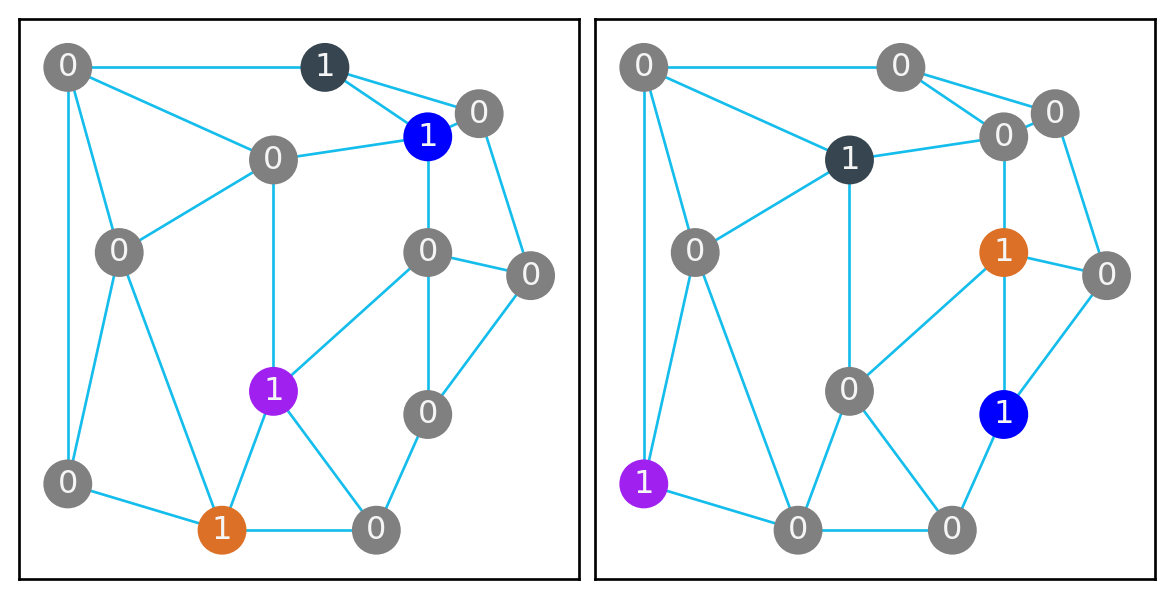
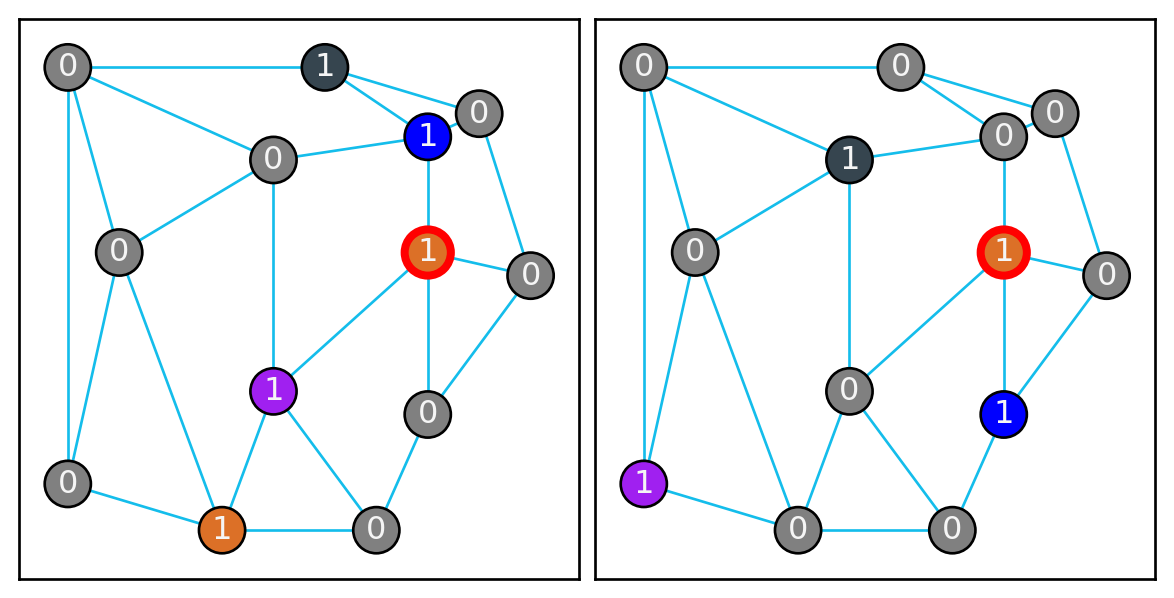
As seen in Figure 3, we can represent the game board as a graph. I’ll look at a simplified version of the game where there are only two types of masters (so that there are two slots in each village). For each type of master, we can have a copy of the graph as in Figure 4.

To show the placement of a master, color the node the player color and set the weight to 1. Increasing the weight of a vertex to 2 will represent showing that there is a student.

Figure 4: In our simplified version we have two types of masters. Player placements of these masters is depicted by two separate graphs, one for each type of master.

For the actions have:

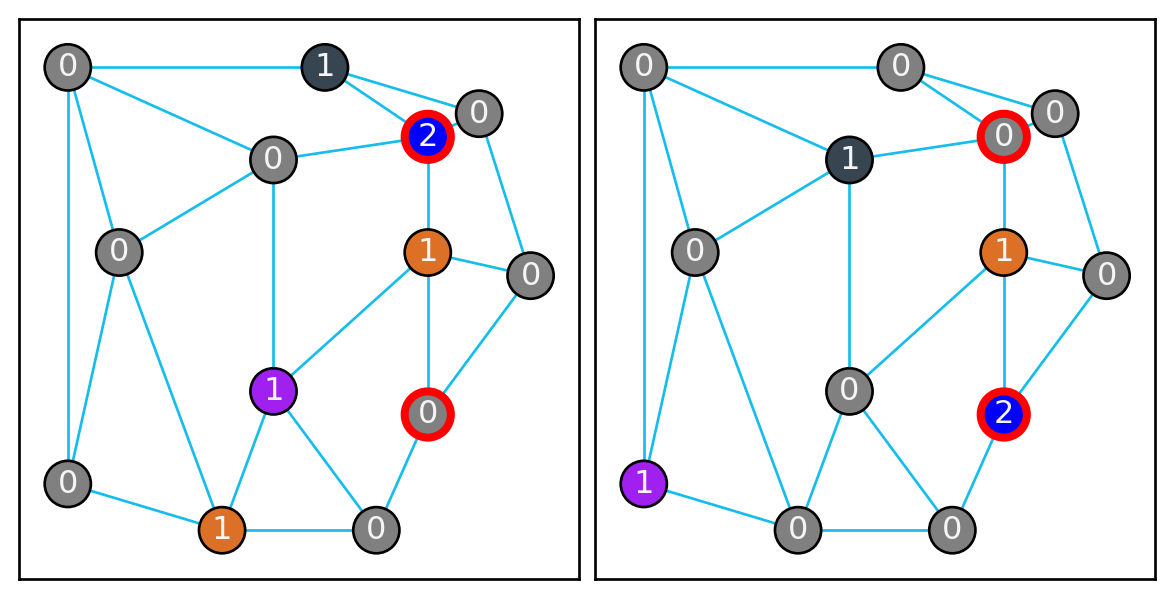
1. Place a master: Choose one of graph copies, and then choose a vertex with weight \(0\), such that the same vertex already has a master of the player’s color in a different graph. Then color it your player color and change it’s weight to 1 (as seen in Figure 5 (a))

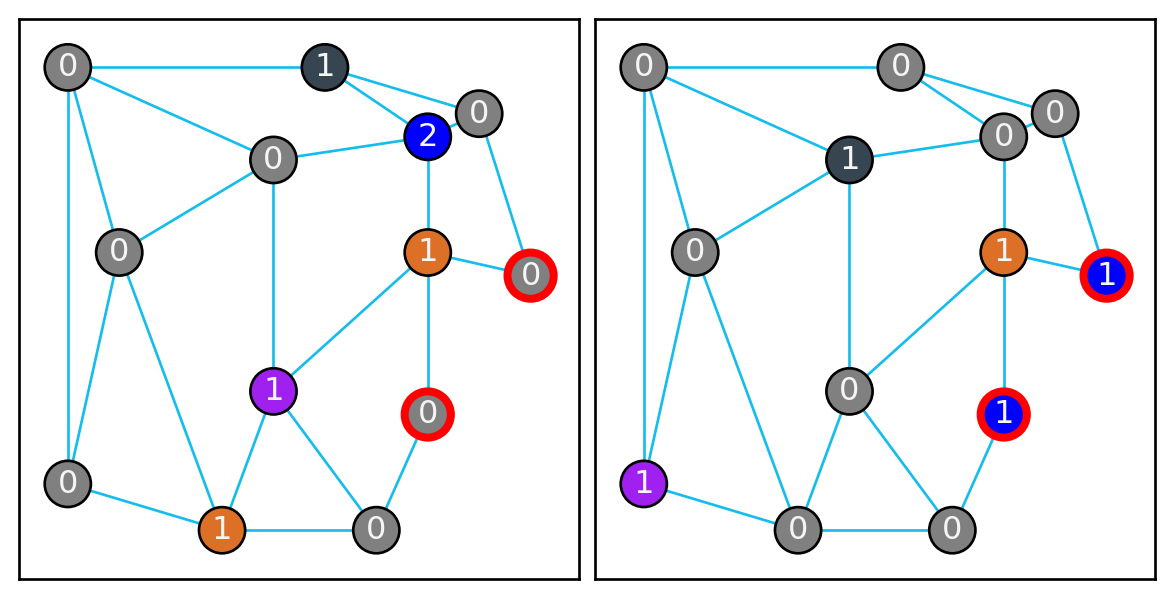
2. Recruit students: Choose two vertices that have your color and are weight \(1\) among the copies. Then increment their weight to \(2\) (as seen in Figure 5 (b))

3. The Journey of the Students: Essentially following the previous rules, with vertices of weight \(2\) interacting and representing the movement of the students. To get the strength of a village, sum the weights of the nodes in all copies of that vertex (the effect is seen in Figure 5 (c)).

(a) Orange placing a master of the first type.

(b) Blue adding a student to each of their masters.

(c) Any player initiating a journey of students.

Figure 5: Showing Bridges of Shangri-La actions in graph form.

Game Analysis

First for the map, we have each vertex has at most 4 edges. That is the degree of a vertex is atmost 4, and in fact \(3 \le deg(v) \le 4,\, \forall v \in V\).

• The fact the number of edges varies a little bit breaks some symmetry, with the right / top-right of the board having smaller degree vertices, and so makes the initial placement a little more meaningful.

Note also that when a spot is filled with a master, it will always be filled. This is because it either gains a master or gets displaced. This is also clear from looking at the weights of a vertex. If a vertex is positive, it will continue to be positive for the rest of the game.

• This means that the game starts to narrow as there are fewer places to a master.

For almost all the discussion above, we haven’t needed graph theory, which begs the question why do any of this? For myself, I think it strips out ancillary (yet important details such as theme, etc.) details and gives a mathematical representation that can be manipulated. Viewing a game through the right lense could be suggestive of some design principals.

For instance, in the above representation I chose to have the game board be represented as multiple copies, with each copy representing a specific type of master / and it’s corresponding slots.

This is interesting because it is suggestive of a game design principle: create independent simple games, and then correlate them / make them interact through a few different actions to add complexity and shared incentives.

Indeed, you can think of the 7 copies as separate games. The master placement rule requires some colocality of changing a vertex (you can only change a weight 0 vertex to weight 1, if it is at least weight 1 and your color in some copy). And the journey of the students requires evaluating the strength of a village. But after that, the student movements/placements can be treated independently.

I think this does several different things:

• With the game being similar to 7 independent subgames, some of the reasoning gets simplified (since different types of masters don’t directly interact).
• Master placement colocality means predicting what an opponent can do is easier. This constraint is useful for making the game more strategic (and also intuitive rules-wise).
• Evaluating the strength of a village directly correlates different types of masters. This allows for shared incentives to emerge with different players.

Another thing is the game can be viewed very coarsely as a series of edge deletions. This then brings up questions for design, by looking at ablations of mathematical properties:

• How does this game feel if some edges are directed?
• What if edge deletion was replaced by other graph operations? For example edge contraction combines two vertices (while removing the edge between them), and retains all the edges coming to/from those vertices. We can mix and match different graph operations and think about how that would influence game play.
• What if edges get deleted / removed for different types of masters? Specifically the journey of the students would delete an edge for some subset of the 7 copies of the graph (rather than all of them), so that certain students can still travel.

Overall, by writing a mathematical representation we can get quite a few ideas on how to modify / get inspired to make games that retain some of the feeling of this one.